Chapter : 2. Force & Laws Of Motion
Law Of Conservation Of Momentum
According to law of conservation of momentum "if there is no force acting on a system, the momentum of the system remains unchanged."
Generalizing the situation " if a group of bodies are exerting force on each other, their total momentum remains conserved before and after the interaction provided there is no external force acting on them."
i.e. m1u1 + m2u2 = m1v1 + m2v2
Example : 7
A rifle of mass 5 kg fires a bullet of mass 40 gm. The bullet leaves the barrel of the rifle with a velocity 200 m/s. If the bullet takes 0.004 s to move through the barrel, calculate the following:
(i) recoil velocity of the rifle and
(ii) the force experienced by the rifle due to its recoil.
Solution. (i) Given mass of the rifle, m1 = 5 kg
Mass of the bullet, m2 = 40 gm = 0.04 kg
Initial velocities, u1 = 0, u2 = 0
After firing velocity of the bullet, v2 = 200 m/s
Velocity of the rifle, v1 = ?
Applying the law of conservation of momentum, we get
m1u1 + m2u2 = m1v1 + m2v2
or 0 + 0 = 5 × v1 + 0.04 × 200
or v1 = – [0.04 × 200]/5 = –1.6 m/s
(ii) Initial momentum of the rifle = 0
Final momentum of the rifle = 5 kg × (–1.6) = –B kg-m/s
Time interval = 0.004 s
∴ Force =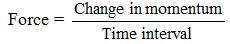
=
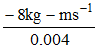= –2000 N
Generalizing the situation " if a group of bodies are exerting force on each other, their total momentum remains conserved before and after the interaction provided there is no external force acting on them."
i.e. m1u1 + m2u2 = m1v1 + m2v2
Example : 7
A rifle of mass 5 kg fires a bullet of mass 40 gm. The bullet leaves the barrel of the rifle with a velocity 200 m/s. If the bullet takes 0.004 s to move through the barrel, calculate the following:
(i) recoil velocity of the rifle and
(ii) the force experienced by the rifle due to its recoil.
Solution. (i) Given mass of the rifle, m1 = 5 kg
Mass of the bullet, m2 = 40 gm = 0.04 kg
Initial velocities, u1 = 0, u2 = 0
After firing velocity of the bullet, v2 = 200 m/s
Velocity of the rifle, v1 = ?
Applying the law of conservation of momentum, we get
m1u1 + m2u2 = m1v1 + m2v2
or 0 + 0 = 5 × v1 + 0.04 × 200
or v1 = – [0.04 × 200]/5 = –1.6 m/s
(ii) Initial momentum of the rifle = 0
Final momentum of the rifle = 5 kg × (–1.6) = –B kg-m/s
Time interval = 0.004 s
∴ Force =
=
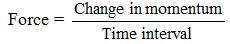
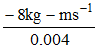= –2000 NTrending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions
Recent Questions Asked
- Newton’s laws of motion asked by Dr. Mukesh Shrimali
- Process of nutrition in Amoeba asked by Rajiv Sharma
- Importance of studying physics subject in school after 10th asked by Rajiv
- Refraction Through Prism in Different Medium asked by Kirti Sharma
- Ratio and Proportion Question asked by Education Desk
- Explain all the 12 tenses with example asked by Qwerty
- Refraction Through Prism in Different Medium asked by Seema Shrimali