Chapter : Polynomial
Examples of a Zeros of a Polynomial
Example: Verify whether the indicated numbers are zeroes of the polynomial corresponding to them in the following cases :
(i) p(x) = 3x + 1, x =
(ii) p(x) = (x + 1) (x – 2), x = – 1, 2
(iii) p(x) = x2, x = 0
(iv) p(x) = lx + m, x = – m/l
(v) p(x) = 2x + 1, x = 1/2
Solution:
(i) p(x) = 3x + 1
→ p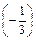 
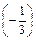= 3 × + 1 = –1 + 1 = 0
∴ x = 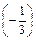is a zero of p(x) = 3x + 1.
(ii) p(x) = (x + 1) (x – 2)
→ p(–1) = (–1 + 1) (–1 – 2) = 0 × –3 = 0 and
→ p(2) = (2 + 1) (2 – 2) = 3 × 0 = 0
∴ x = –1 and x = 2 are zeroes of the given polynomial.
(iii) p(x) = x2 → p(0) = 02 = 0
∴ x = 0 is a zero of the given polynomial
(iv) p(x) = lx + m → p = l
+ m = – m + m = 0
∴ x = is a zero of the given polynomial.
(v) p(x) = 2x + 1 → p = 2(1/2) × + 1 = 1 + 1 = 2 ¹ 0
∴ x = 1/2 is not a zero of the given polynomial.
Example: Find the zero of the polynomial in each of the following cases :
(i) p(x) = x + 5
(ii) p(x) = 2x + 5
(iii) p(x) = 3x – 2
Solution: To find the zero of a polynomial p(x) means to solve the polynomial equation p(x) = 0.
(i) For the zero of polynomial p(x) = x + 5
p(x) = 0 → x + 5 = 0 → x = –5
∴ x = –5 is a zero of the polynomial p(x) = x + 5.
(ii) p(x) = 0 → 2x + 5 = 0
→ 2x = –5 and x =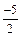 
∴ x =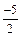 is a zero of p(x) = 2x + 5.
(iii) p(x) = 0 → 3x – 2 = 0
→ 3x = 2 and x =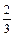 
.
∴ x = 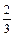is zero of p(x) = 3x – 2
Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions
Recent Questions Asked
- Newton’s laws of motion asked by Dr. Mukesh Shrimali
- Process of nutrition in Amoeba asked by Rajiv Sharma
- Importance of studying physics subject in school after 10th asked by Rajiv
- Refraction Through Prism in Different Medium asked by Kirti Sharma
- Ratio and Proportion Question asked by Education Desk
- Explain all the 12 tenses with example asked by Qwerty
- Refraction Through Prism in Different Medium asked by Seema Shrimali