Mathematics

To Understand the concept of Geometric Meaning of the Zeros of a Polynomial. Let us consider linear polynomial ax + b. The graph of y = ax + b is a straight line.
For example : The graph of y = 3x + 4 is a straight line passing through (0, 4) and (2, 10).

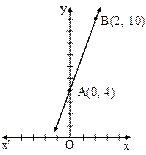
(i) Let us consider the graph of y = 2x – 4 intersects the x-axis at x = 2. The zero 2x – 4 is 2. Thus, the zero of the polynomial 2x – 4 is the x-coordinate of the point where the graph y = 2x – 4 intersects the x-axis.

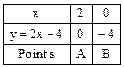
(ii) A general equation of a linear polynomial is ax + b. The graph of y = ax + b is a straight line which intersects the x-axis at 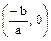. Zero of the polynomial ax + b is the x-coordinate of the point of intersection of the graph with x-axis.

(iii) Let us consider the quadratic polynomial x² – 4x + 3. The graph of x² – 4x + 3 intersects the x-axis at the point (1, 0) and (3, 0).
Zeroes of the polynomial x² – 4x + 3 are the x-coordinates of the points of intersection of the graph with x-axis.

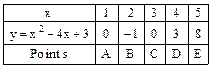
The shape of the graph of the quadratic polynomials is ∪ and the curve is known as parabola.

(iv) Now let us consider one more polynomial –x² + 2x + 8. Graph of this polynomial intersects the x-axis at the points (4, 0), (–2, 0). Zeroes of the polynomial –x² + 2x + 8 are the x-coordinates of the points at which the graph intersects the x-axis. The shape of the graph of the given quadratic polynomial is ∩ and the curve is known as parabola.

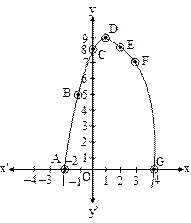
The zeroes of a quadratic polynomial ax² + bx + c he x-coordinates of the points where the graph of y = ax² + bx + c intersects the x-axis.
Cubic polynomial : Let us find out geometrically how many zeroes a cubic has. To understand this let consider cubic polynomial x³ – 6x² + 11x – 6.

Case 1 : The graph of the cubic equation intersects the x-axis at three points (1, 0), (2, 0) and (3, 0). Zeroes of the given polynomial are the x-coordinates of the points of intersection with the x-axis.

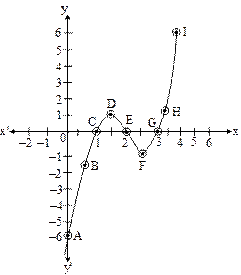
Case 2 : The cubic equation x³ – x² intersects the x-axis at the point (0, 0) and (1, 0). Zero of a polynomial x³ – x² are the x-coordinates of the point where the graph cuts the x-axis. Zeroes of the cubic polynomial are 0 and 1.

Case 3 : Let us consider the equation of cubic polynomial y = x³. Cubic polynomial has only one zero.

In short, we say that, a cubic equation can have 1 or 2 or 3 zeroes or any polynomial of degree three can have at most three zeroes.

Important Note: In general, polynomial of degree n, the graph of y = p(x) passes x-axis at most at n points. Therefore, a polynomial p(x) of degree n has at most n zeroes.