Given equation f(x) = x3 – 3x – 5
Differentiate with respect to x, we get f ‘(x) = 3x2 – 3
Now, first find the range, where the real roots lie in i.e. f(2) = –3 and f(3) = 13
Since f(2) is a negative value and f(3) is a positive value. Therefore, our one real root of the equation lies between x = 2 and 3.
Now, by Newton-Raphson formula
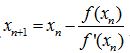
Now, substitute the value of f(x) and f'(x) in this formula

Choose the initial approximate value of the root x0 = 2 and putting n = 0, we have the first approximate value
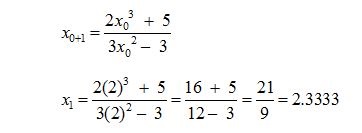
Now, for the second approximation, replacing n = 1 in equation (1) we get
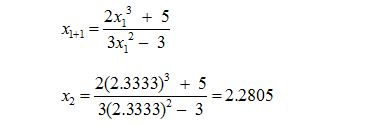
Now, for the third approximation, replacing n = 2 in equation (1) we get
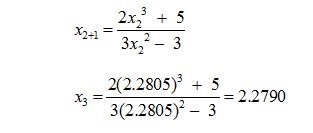
Now, for the Fourth approximation, replacing n = 3 in equation (1) we get
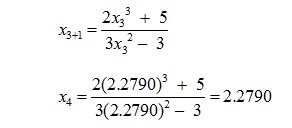
Here x3 and x4 obtained the same value; therefore one root of the given equation = x3 – 3x – 5 using the Newton Raphson Method is 2.2790.
Read More Articles – See tips by experts
- How to get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- Physics & Maths tutor helps to improve your child’s knowledge
- 5 Important tips to Personal Development apply in your daily life
- Reasons to attempt ONLINE MOCK TEST SERIES for Bank PO Exams
Please login or Register to submit your answer
