What is the sum of the series and what is the work of sigma notation in it

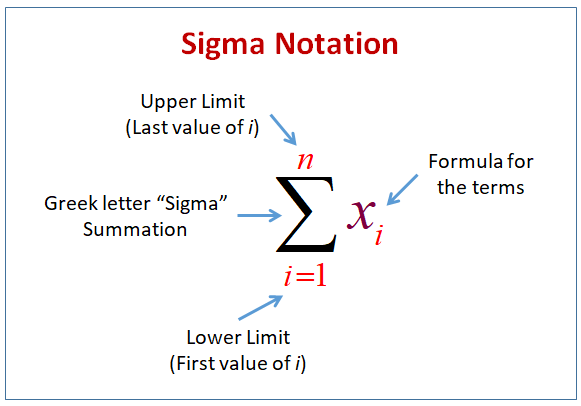
In mathematics, the sum of the series is used widely in the topic of the sequence and the series. Sequence and series are referred to the terms to be added or subtracted equally and form a bulk of numbers in increasing or decreasing order.

In the sum of the series, the notation of the sigma is used for making the work easier for reading and writing the large terms of the sequence and the series. In this post, we will learn about the sum of the series, sigma notation, and a lot of examples to understand these concepts.

What is the sum of the series?

The term series referred to the sequence of the terms either increasing or decreasing by adding or subtracting the equal length of numbers in a number. The sequence is the same as the series in working. But there is a little bit difference between these two terms.

The difference is that in the sequence we use commas to separate the terms while in series we have to use the sum sign between the terms. For example, the set of the numbers in the form of 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20 is said to be the sequence with the equal difference of two among the digits.

While the set of numbers in the form of 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 is said to be the series of the terms of the first ten even numbers. In general, we can write,

Sequence = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20

Series = 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20

The equation of the sum of the series can be written by using sigma notation as,

In the equation of the sum of the series, n is the total number of the terms, x is the starting value of the series and f(x) is the series of the numbers.

What is the working of sigma notation in the sum of the series?

The working of the sigma notation is very essential in the sum of the series for avoiding the large numbers of the terms in the series. The sigma notation enclosed the large numbers of series in it. By taking the sigma notation from the initial and the final number.

Let’s take a bulk of examples to understand this concept more accurately.

Example 1 : Convert the given series in the form of the sigma notation,

2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30

Solution

Step 1: Take the given sum of the series.

2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30

Step 2: Take the common difference among the terms and make a function.

Common difference = 2

Function = f(x) = 2x

Step 3: Now take the general form of the sum of the series.

Step 4: Put the value of the function and the total number of the terms and the starting value.

Step 5: Write the series with the result.

 = 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30

How to calculate the sum of the series?

The Sum of the series is calculated by applying the sigma values to the function one by one. Apply the values of sigma notation from initial to the final one by one and then add all the outputs to get the sum of the series. The Sum of the series can be calculated easily by using the sum of series calculator.

Example 1

Solve (x + 1) – 7

Solution

Step 1: Identify the terms and function of the sigma notation.

Values 1 to 9 = 1, 2, 3, 4, 5, 6, 7, 8, 9

Equation = x (x + 1) – 7

Step 2: put the values in equation one by one.

When x = 1

x (x + 1) – 7 = 1(1 + 1) – 7 = 1(2) – 7 = 2 – 7 = -5

When x = 2

x (x + 1) – 7 = 2(2 + 1) – 7 = 2(3) – 7 = 6 – 7 = -1

When x = 3

x (x + 1) – 7 = 3(3 + 1) – 7 = 3(4) – 7 = 12 – 7 = 5

When x = 4

x (x + 1) – 7 = 4(4 + 1) – 7 = 4(5) – 7 = 20 – 7 = 13

When x = 5

x (x + 1) – 7 = 5(5 + 1) – 7 = 5(6) – 7 = 30 – 7 = 23

When x = 6

x (x + 1) – 7 = 6(6 + 1) – 7 = 6(7) – 7 = 42 – 7 = 35

When x = 7

x (x + 1) – 7 = 7(7 + 1) – 7 = 7(8) – 7 = 56 – 7 = 49

When x = 8

x (x + 1) – 7 = 8(8 + 1) – 7 = 8(9) – 7 = 72 – 7 = 65

When x = 9

x (x + 1) – 7 = 9(1 + 1) – 7 = 9(10) – 7 = 90 – 7 = 83

Step 3: Now add all the outputs of the sigma by applying the values from initial to final.

-5 – 1 + 5 + 13 + 23 + 35 + 49 + 65 + 83 = 267

Step 4: Write the output with the given input in the form of sigma notation.

(x + 1) – 7 = 267

Summary

The series is a very useful topic used in mathematics. Now you can solve any kind of problem related to this topic. By following the above examples, all the problems become easy for you.

Also read : NTSE Mathematics