Chapter : Motion in one Dimension
Acceleration
It is defined as the rate of change of velocity.
(i) It is a vector quantity.
(ii) Its direction is same as that of change in velocity and not of the velocity (That is why acceleration in circular motion is towards the centre)
(iii) There are three ways possible in which change in velocity may occur
Types of acceleration :
(a) Instantaneous acceleration :
It is defined as the acceleration of a body at some particular instant.
Instantaneous acceleration =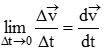
(b) Average acceleration :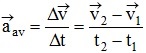
(c) Uniform acceleration : A body is said to have uniform acceleration if magnitude and direction of the acceleration remains constant during particle motion.
Note : If a particle is moving with uniform acceleration, this does not necessarily imply that particle is moving in straight line.
Example : Parabolic motion
(d) Non-uniform acceleration :
A body is said to have non-uniform acceleration, if magnitude or direction or both change during motion.
Note :
(i) Acceleration is a vector with dimensions [LT–2] and SI units (m/s2)
(ii) If acceleration is zero, velocity will be constant and motion will be uniform.
(iii) However if acceleration is constant then acceleration is uniform but motion is non-uniform and if acceleration is not constant then both motion and acceleration are non-uniform.
(iv) If a force acts on a particle of mass m then by Newton's II law
acts on a particle of mass m then by Newton's II law 
(v) As by definition
i.e. if is given as a function of time, second time derivative of displacement gives acceleration.
is given as a function of time, second time derivative of displacement gives acceleration.
(vi) If velocity is given as function of position then by chain rule

(vii) As acceleration the slope of velocity-time graph gives acceleration i.e.
the slope of velocity-time graph gives acceleration i.e.
 = tan θ
= tan θ
(viii) The slope of -t curve, i.e.
-t curve, i.e. 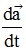 is a measure of rate of non-uniformity of acceleration. However we do not define this physical quantity as it is not involved in basic laws or equation of motion.
is a measure of rate of non-uniformity of acceleration. However we do not define this physical quantity as it is not involved in basic laws or equation of motion.
(ix) Acceleration can be positive or negative. Positive acceleration means velocity is increasing with time while negative acceleration called retardation means velocity is decreasing with time.
(i) It is a vector quantity.
(ii) Its direction is same as that of change in velocity and not of the velocity (That is why acceleration in circular motion is towards the centre)
(iii) There are three ways possible in which change in velocity may occur
| When only direction | When only magnitude changes | When both the direction changes and magnitude change |
|---|---|---|
| To change the direction net acceleration or net force should be perpendicular to direction of velocity Example: Uniform circular motion | In this case, net force or net acceleration should be parallel or anti-parallel to the direction of velocity. (straight line motion) Example: When ball is thrown up under gravity. | In this case, net force or net acceleration has two components. One component is parallel or anti-parallel to velocity and another one is perpendicular to velocity Example : Projectile motion |
(a) Instantaneous acceleration :
It is defined as the acceleration of a body at some particular instant.
Instantaneous acceleration =
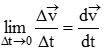
(b) Average acceleration :
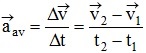
(c) Uniform acceleration : A body is said to have uniform acceleration if magnitude and direction of the acceleration remains constant during particle motion.
Note : If a particle is moving with uniform acceleration, this does not necessarily imply that particle is moving in straight line.
Example : Parabolic motion
(d) Non-uniform acceleration :
A body is said to have non-uniform acceleration, if magnitude or direction or both change during motion.
Note :
(i) Acceleration is a vector with dimensions [LT–2] and SI units (m/s2)
(ii) If acceleration is zero, velocity will be constant and motion will be uniform.
(iii) However if acceleration is constant then acceleration is uniform but motion is non-uniform and if acceleration is not constant then both motion and acceleration are non-uniform.
(iv) If a force
 acts on a particle of mass m then by Newton's II law
acts on a particle of mass m then by Newton's II law 
(v) As by definition

i.e. if
 is given as a function of time, second time derivative of displacement gives acceleration.
is given as a function of time, second time derivative of displacement gives acceleration.(vi) If velocity is given as function of position then by chain rule

(vii) As acceleration
 the slope of velocity-time graph gives acceleration i.e.
the slope of velocity-time graph gives acceleration i.e.  = tan θ
= tan θ (viii) The slope of
 -t curve, i.e.
-t curve, i.e. 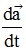 is a measure of rate of non-uniformity of acceleration. However we do not define this physical quantity as it is not involved in basic laws or equation of motion.
is a measure of rate of non-uniformity of acceleration. However we do not define this physical quantity as it is not involved in basic laws or equation of motion.(ix) Acceleration can be positive or negative. Positive acceleration means velocity is increasing with time while negative acceleration called retardation means velocity is decreasing with time.
Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions