9. Motion of a body on a smooth inclined plane
A body is placed on a smooth inclined plane AB which makes an angle q with the horizontal. The forces acting on body are

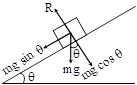
(i) Weight of the body mg acting vertically down.
(ii) Normal reaction R acting perpendicular to the plane.
The weight mg of the body is resolved parallel and perpendicular to the plane as mg sin θ parallel to the plane and mg cos θ perpendicular to the plane.
Thus ma = mg sin θ ⇒ a = g sin θ ...(i)
R = mg cos θ ...(ii)
Note:
The same result can also be obtained by resolving the forces horizontally and vertically.
R sin θ = ma cos θ
mg – R cos θ = ma sin θ
solving we get,
a = g sin θ, R = mg cos θ
Special case :
When the smooth plane is moving horizontally with an acceleration (b) as shown in fig

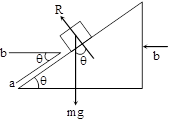
In this case :
m (a + b cos θ) = mg sin θ
and mb sin θ = R – mg cos θ
solving we get a = g sin θ – b cos θ
R = m (g cos θ + b sin θ)