Chapter : Circular Motion & Rotational Dynamics
10. Moment of Inertia (Rotational inertia)
10. Moment of Inertia (Rotational inertia)
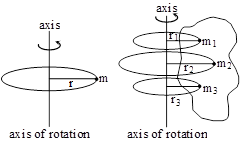
(a) The virtue, by which a body revolving about an axis opposes the change in rotational motion, is known as moment of inertia.
(b) The moment of inertia of a particle with respect to an axis of rotation is equal to the product of mass of the particle and square of distance from the axis, hence I = mr2
(c) The moment of inertia of a system about an axis of rotation is equal to the sum of moment of inertia of all the particles of the system about the axis of rotation.
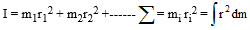
(d) It is a scalar quantity
(e) Unit : in M. K. S = kg-m2 and in C.G.S = gm-cm2
(f) Dimension : [M1L2T0]
(g) Moment of inertia depends on the following factors.
i) Mass of body
ii) Mass distribution of body or shape, size, density of body.
iii) On the position of axis of rotation.
Note : The more is the distribution of mass with respect to axis of rotation the more will be moment of inertia.
(h) Moment of inertia does not depend on the following factors.
i) Angular velocity (ω)
ii) Angular Acceleration (α)
iii) Torque (τ)
vi) Angular Momentum (J)
10.1 Radius of Gyration - (K)
(a) The distance, from the axis of rotation where, the entire mass of the body is supposed to be concentrated and the value of moment of inertia is same as that due to actual distribution of masses of body, is called radius of gyration.
(b) The radius of gyration of a body about different axes is different
(c) If K be the radius of gyration, I = mK2
⇒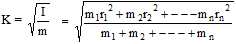
(d) For a symmetrical body, the radius of gyration is equal to the root mean square of distances of all the particles from the axis of rotation. or if, m1 = m2 = ----------- = mn
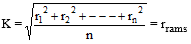
(e) The value of radius of gyration depends upon the axis of rotation and mass distribution with respect to it
(f) Radius of gyration does not depend upon mass of body.
10.2 Theorems of moment of inertia
(a) Theorem of perpendicular axis -
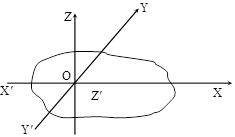
According to this theorem the moment of inertia of a lamina about an axis passing through its axis and perpendicular to its plane is equal to the sum of moment of inertia about the two mutually perpendicular axis in the plane of lamina. The normal axis OZ must pass through the point intersection of two mutually perpendicular axes ox and oy.
Izz'= Ixx' + Iyy'
Note: This theorem is used only for plane lamina.
(b) Theorem of parallel axes :-
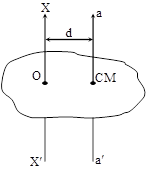
According to this theorem, the moment of inertia of a body about any axis is equal to the sum of moment of inertia about an axis passing through its centre of gravity and parallel to given axis and product of its mass and square of distance between the centre of gravity and the axis of rotation.
Ixx' = IC.G + Md2
(c) The moment of inertia of two point masses about their centre of mass -
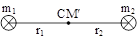
Let m1 and m2 be two masses distant r from each other and r1 and r2 be the distances of their centre of mass from m1 to m2 respectively.
1) r1 + r2 = r
2) m1r1 = m2r2
3) r1 =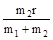 , r2=
, r2= 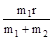
4) I = m1r12 + m2r22
5) I = r2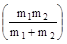 = μr2
= μr2
where m =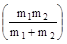 is known as reduced mass μ < m1 and μ < m2
is known as reduced mass μ < m1 and μ < m2
6) In Diatomic molecules like H2, HCl etc. moment of inertia about there center of mass is derived from above formula.

(a) The virtue, by which a body revolving about an axis opposes the change in rotational motion, is known as moment of inertia.
(b) The moment of inertia of a particle with respect to an axis of rotation is equal to the product of mass of the particle and square of distance from the axis, hence I = mr2
(c) The moment of inertia of a system about an axis of rotation is equal to the sum of moment of inertia of all the particles of the system about the axis of rotation.
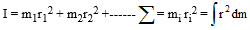
(d) It is a scalar quantity
(e) Unit : in M. K. S = kg-m2 and in C.G.S = gm-cm2
(f) Dimension : [M1L2T0]
(g) Moment of inertia depends on the following factors.
i) Mass of body
ii) Mass distribution of body or shape, size, density of body.
iii) On the position of axis of rotation.
Note : The more is the distribution of mass with respect to axis of rotation the more will be moment of inertia.
(h) Moment of inertia does not depend on the following factors.
i) Angular velocity (ω)
ii) Angular Acceleration (α)
iii) Torque (τ)
vi) Angular Momentum (J)
10.1 Radius of Gyration - (K)
(a) The distance, from the axis of rotation where, the entire mass of the body is supposed to be concentrated and the value of moment of inertia is same as that due to actual distribution of masses of body, is called radius of gyration.
(b) The radius of gyration of a body about different axes is different
(c) If K be the radius of gyration, I = mK2
⇒
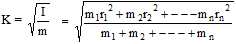
(d) For a symmetrical body, the radius of gyration is equal to the root mean square of distances of all the particles from the axis of rotation. or if, m1 = m2 = ----------- = mn
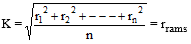
(e) The value of radius of gyration depends upon the axis of rotation and mass distribution with respect to it
(f) Radius of gyration does not depend upon mass of body.
10.2 Theorems of moment of inertia
(a) Theorem of perpendicular axis -

According to this theorem the moment of inertia of a lamina about an axis passing through its axis and perpendicular to its plane is equal to the sum of moment of inertia about the two mutually perpendicular axis in the plane of lamina. The normal axis OZ must pass through the point intersection of two mutually perpendicular axes ox and oy.
Izz'= Ixx' + Iyy'
Note: This theorem is used only for plane lamina.
(b) Theorem of parallel axes :-

According to this theorem, the moment of inertia of a body about any axis is equal to the sum of moment of inertia about an axis passing through its centre of gravity and parallel to given axis and product of its mass and square of distance between the centre of gravity and the axis of rotation.
Ixx' = IC.G + Md2
(c) The moment of inertia of two point masses about their centre of mass -
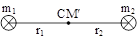
Let m1 and m2 be two masses distant r from each other and r1 and r2 be the distances of their centre of mass from m1 to m2 respectively.
1) r1 + r2 = r
2) m1r1 = m2r2
3) r1 =
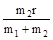 , r2=
, r2= 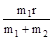
4) I = m1r12 + m2r22
5) I = r2
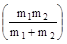 = μr2
= μr2 where m =
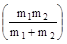 is known as reduced mass μ < m1 and μ < m2
is known as reduced mass μ < m1 and μ < m2 6) In Diatomic molecules like H2, HCl etc. moment of inertia about there center of mass is derived from above formula.
Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions