Chapter : Circular Motion & Rotational Dynamics
3. Relation Between Linear Velocity And Angular Velocity
3. Relation between linear velocity and angular velocity
We have
[∴ dθ = , angle =
, angle =  and v =
and v = 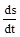 = linear velocity]
= linear velocity]
⇒ v = rω
In vector form,
Note :
(i) When a particle moves along a curved path, its linear velocity at a point is along the tangent drawn at that point
(ii) When a particle moves along curved path, its velocity has two components. One along the radius, which increases or decreases the radius and another one perpendicular to the radius, which makes the particle to revolve about the point of observation.
(iii)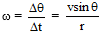
We have

[∴ dθ =
 , angle =
, angle =  and v =
and v = 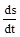 = linear velocity]
= linear velocity]⇒ v = rω
In vector form,

Note :
(i) When a particle moves along a curved path, its linear velocity at a point is along the tangent drawn at that point
(ii) When a particle moves along curved path, its velocity has two components. One along the radius, which increases or decreases the radius and another one perpendicular to the radius, which makes the particle to revolve about the point of observation.
(iii)
Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions