Chapter : Newton's Laws Of Motion & Friction
10. Motion of two bodies connected by a string
10. Motion of two bodies connected by a string Case (A) : Motion of unequal masses suspended from a light frictionless pulley:
A and B are two bodies of mass m1and m2 respectively suspended by means of a light string passing over a smooth pulley P.

Let m2 > m1. If the string is light and continuous a tension T exists all along the string. The forces acting on A and B are clearly shown. Let A moves up with an acceleration a and B move down with the same acceleration.
For the motion of A
T – m1g = m1a ...(i)
For the motion of B
m2g – T = m2a ...(ii)
Solving,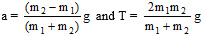
Case (B) : Let us consider the case of a body of mass (m1), to which a light and string is attached rests on a smooth horizontal plane. The string passes over a frictionless pulley fixed at the end of plane. Another end of the string carries a mass ( m2 ) as shown in fig. Our aim is to calculate the acceleration of the system and tension in the string :
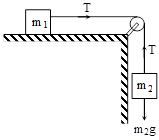
Here We have
(m2g – T ) = m2a ....(1)
and T = m1a ....(2)
Solving these equations we have,
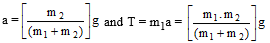
Case (C) : Here we shall consider the above case with a difference that (m1) placed on smooth inclined plane making an angle(θ) with horizontal as shown in fig. :
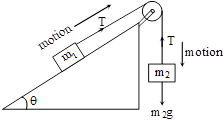
In this case
T – m1g sin θ = m1a
and (m2g – T) = m2a
solving we get,

Case (D) : Let us consider the case when masses (m1) and (m2) are on inclined plane making angles (α) and (β) with horizontal respectively as shown in figure :
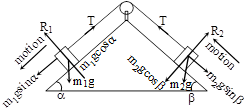
We have, m1g sin α – T = m1a
and T – m2 g sin β = m2 a
solving these equations we get,

A and B are two bodies of mass m1and m2 respectively suspended by means of a light string passing over a smooth pulley P.

Let m2 > m1. If the string is light and continuous a tension T exists all along the string. The forces acting on A and B are clearly shown. Let A moves up with an acceleration a and B move down with the same acceleration.
For the motion of A
T – m1g = m1a ...(i)
For the motion of B
m2g – T = m2a ...(ii)
Solving,
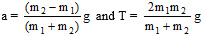
Case (B) : Let us consider the case of a body of mass (m1), to which a light and string is attached rests on a smooth horizontal plane. The string passes over a frictionless pulley fixed at the end of plane. Another end of the string carries a mass ( m2 ) as shown in fig. Our aim is to calculate the acceleration of the system and tension in the string :

Here We have
(m2g – T ) = m2a ....(1)
and T = m1a ....(2)
Solving these equations we have,
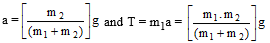
Case (C) : Here we shall consider the above case with a difference that (m1) placed on smooth inclined plane making an angle(θ) with horizontal as shown in fig. :

In this case
T – m1g sin θ = m1a
and (m2g – T) = m2a
solving we get,

Case (D) : Let us consider the case when masses (m1) and (m2) are on inclined plane making angles (α) and (β) with horizontal respectively as shown in figure :

We have, m1g sin α – T = m1a
and T – m2 g sin β = m2 a
solving these equations we get,

Trending Articles & Blogs
- Physics Tutor, Math Tutor Improve Your Child’s Knowledge
- How to Get Maximum Marks in Examination Preparation Strategy by Dr. Mukesh Shrimali
- 5 Important Tips To Personal Development Apply In Your Daily Life
- Breaking the Barriers Between High School and Higher Education
- 14 Vocational courses after class 12th
- Tips to Get Maximum Marks in Physics Examination
- Get Full Marks in Biology Class 12 CBSE
Download Old Sample Papers For Class X & XII
Download Practical Solutions of Chemistry and Physics for Class 12 with Solutions